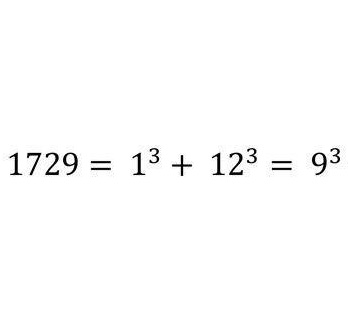Скільки разів можна від 100 відняти 10?

Мозаїка з трикутників

Полічіть, скільки трикутників у фігурі, яка зображена на малюнку:

Складність головоломки: 6.

Вовк, коза і капуста

Microsoft Mathematics 4.0 являє собою графічний калькулятор, що будує двовимірні та тривимірні графіки, забезпечує покрокове розв’язання рівнянь, надає доступ до корисних інструментів, призначених для розв’язання математичних задач, а також задач з інших предметів.

Використовуючи дану програму учні мають нагоду навчитися розв’язувати рівняння крок за кроком, отримати кращі уявлення про основи алгебри, тригонометрії, математичних обчислень, фізики та хімії.

Четверта версія програми Microsoft Mathematics налічує цілий ряд вдосконалень, включаючи наступні:

• Покращений математичний двигун
  • Обчислювальний двигун
  • Графічний двигун
• Новий інструмент вводу даний
  • Надійніше розпізнання рукописного тексту
  • Засіб корекції
• Вдосконалений інтерфейс
  • Стрічка
  • Оформлення в стилі додатків MS Office

За допомогою даного навчального програмного засобу учні не лише навчаються розв’язувати рівняння, але й отримують більш глибоке розуміння базових понять і елементів математики, точних наук і предметів природничого циклу.

Центральним елементом навчального програмного засобу є повнофункціональнийГрафічний Калькулятор з його широкими можливостями в сфері побудови графічних об’єктів та вирішення рівнянь. Він відкриває великий спектр додаткових інструментів, який сприяє поглибленому розумінню учнями найскладніших явищ математики та інших навчальних дисциплін.

Використовуючи Покрокові Математичні Рішення, учні отримують настанови щодо розв’язання завдань з різноманітних предметів, починаючи з основ алгебри та обчислень. Це дозволяє їм розв’язувати рівняння більш швидко й ефективно.

Бібліотека Формул і Рівнянь містить збірку більш ніж 100 найбільш вживаних математичних рівнянь і формул, яка уможливлює процес ідентифікації та відповідного застосування рівняння, що необхідне для розв’язання математичних та інших завдань.

Трикутник (програма для розв’язання задач з трикутниками) є графічним інструментом, що може бути використаний учнями для розгляду трикутників, кращого розуміння відношення різних частин трикутника з метою знаходження сторін, кутів, формул і значень.

Інструмент Перетворення Одиниць дозволяє учням швидко і легко конвертувати одиниці виміру, що охоплюють такі сфери, як довжина, площа, об’єм,  вага, температура, тиск, потужність, час, швидкість, енергія.

Нова функція Підтримка Рукописного Вводу (для планшетних та мобільних персональних комп’ютерів) надає учням можливість робити нотатки від руки, спрощуючи оперування програмою Microsoft Mathematics 4.0.

Microsoft Mathematics доступний для завантаження абсолютно безкоштовно — Завантажити Microsoft Mathematics.

Особливо важливу роль під час розв'язування стереометричних задач відіграють малюнки. Але малюнок тут — не мета, а тільки допоміжний засіб. Якщо учень може розв'язати задачу без малюнка, він може його й не виконувати.

Розв'язання переважної більшості стереометричних задач, поданих в учнівських навчальних посібниках, бажано супроводити малюнками. Треба намагатись, щоб малюнки були правильними, наочними і щоб їх легко можна було виконувати. Іноді вважають, що учнівські малюнки до стереометричних задач повинні бути також повними і метрично визначеними. Однак не слід вимагати виконувати такі малюнки до кожної задачі. До тієї самої задачі можна пропонувати той чи інший малюнок.

Деякі вчителі різні просторові фігури іноді зображають на частинах площини. В окремих випадках можна малювати не всю просторову фігуру, а її осьовий переріз або одну з кількох секцій, або лінію перетину фігур. Не обов'язково малювати всі вектори, про які йдеться в розв'язанні задачі. Замість кулі, вписаної або описаної навколо многогранника, можна малювати коло великого круга, а в деяких випадках — тільки центр і окремі точки її поверхні.

У зошитах учні можуть виконувати малюнки олівцем, але зобов'язувати всіх малювати тільки олівцем було б неправильно. Непогано, коли окремі учні малюють ручкою або фломастерами. Малюючи на дошці, можна використовувати різноколірну крейду, особливо під час розв'язування задач на комбінації тіл, на побудову. Звичайно пропонують учням користуватись лінійкою та іншими креслярськими інструментами. Але треба, щоб вони вміли малювати і від руки.

Виконуючи малюнки до стереометричних задач, слід дотримуватись правил і вимог, встановлених у кресленні. Зокрема слід використовувати такі види ліній:

• суцільна основна,
• суцільна потовщена,
• суцільна тонка,
• штрихова,
• штрихпунктирна.

Суцільними основними обводять лінії видимого контура фігури, потовщеними користуються для виділення тієї чи іншої частини фігури, суцільні тонкі використовують як розмірні і виносні лінії, для штриховки тощо. Штриховими малюють лінії невидимих контурів, штрих пунктирними — осьові та центральні лінії.

Не слід штриховку (перерізів) робити штриховими лініями, не треба розривати розмірні лінії. Еліпси можна малювати від руки або за допомогою спеціальних лекал.

На малюнках можна позначати значення довжин, величини кутів, прямі кути, рівні відрізки тощо. Букви і цифри слід писати так, щоб вони не перетинали ліній.

Джерело: Г. П. Бевз. «Методика розв’язування стереометричних задач». Київ 1988

У процесі навчання математики задачі відіграють велику й багатопланову роль.

Розв'язування задач добре служить досягненню тих цілей, які ставляться перед навчанням математики в середній школі. Саме тому більше половини уроків математики відводиться розв'язуванню задач та виконанню вправ.

Розв'язуючи задачі, учні засвоюють найважливіші математичні поняття, оволодівають математичною символікою, навчаються виконувати доведення тощо.

Крім того, математичні задачі можуть готувати до засвоєння нових теоретичних питань, допомагати закріпленню здобутих знань, ілюструвати практичні застосування вивченого матеріалу. У процесі розв'язування задач в учнів формуються навички розумової праці, а також важливі риси характеру: наполегливість, уважність, зосередженість.

Сформулюємо основні положення методики розв'язування стереометричних задач:

1.  На уроках стереометрії бажано більше навчати учнів розв'язувати задачі за зразками.

2.   Вчити учнів розв'язувати задачі доцільно за типами.

3.   Задачі кожного нового типу слід починати розв'язувати з найпростіших, поступово переходячи до складніших.

4.   Понад половини стереометричних задач доцільно розв'язувати з учнями усно.

5.  Для розвитку просторової уяви і графічної культури учнів на початку опрацювання кожної нової теми слід пропонувати вправи на малювання відповідних фігур.

6.  Малюнок в розв'язанні стереометричної задачі — не мета, а допоміжний засіб. Переважну більшість таких малюнків на класній дошці можна виконувати від руки.

7.  Кількості задач на обчислення, побудову, доведення і дослідження, пропонованих старшокласникам, повинні приблизно відноситись як 2:1:1:1.

8.   Значну увагу потрібно приділити колективній формі розв'язування задач у класі. (Якщо учень ще не навчився розв'язувати задачі того чи іншого типу, не слід пропонувати йому розв'язувати їх самостійно).

9.   Найвідповідальніші етапи в колективному розв'язуванні задачі — її вивчення і складання плану розв'язання. Не слід економити час за рахунок ущільнення цих етапів.

10.  Після розв'язування окремих задач бажано робити узагальнення, відмічати цікаві частинні випадки, виділяти групи подібних задач.

11.  Для деяких задач бажано пропонувати учням тільки виконати малюнок і скласти план розв'язання, не розв'язуючи задачу до кінця.

12.  Бажано максимально заохочувати пошуки різних способів розв'язання задач, знаходити серед них найраціональніші.

13.  До моделювання корисно звертатися тільки тоді, коли без цього учні не можуть правильно уявити зміст задачі.

14.  Самостійні роботи по розв'язуванню стереометричних задач не слід плутати з контрольними роботами. Основна мета самостійної роботи — навчати, удосконалювати уміння і навички учнів, а не контролювати.

15.  Більше уваги прикладним задачам.

16.  Менше формалізму в оформленнях розв'язань стереометричних задач, особливо на випускних екзаменах.

17.  Частіше пропонувати учням задачі на моделях.

Раціональна методика навчання розв'язуванню математичних задач відіграє істотну роль у формуванні високого рівня математичних знань, умінь і навичок учнів.

Все, що тобі потрібно

Натисніть на картинку для збільшення розміру зображення.

Портал в математиці

Натисніть на картинку для збільшення розміру зображення.

Одного разу математик Годфрі Харді відправився відвідати хворого математика Срініваса Рамануджана. Після прибуття Харді зауважив, що приїхав на таксі «з досить нудним номером» 1729. На це Рамануджан негайно заперечив, що 1729 - дуже цікаве число. Це мінімальне число з натуральних, для якого існує більше одного розкладання в суму двох кубів. Завдяки цій історії такі числа (тобто ті, що можна представити у вигляді суми двох кубів декількома способами) отримали найменування чисел таксі.

Натисніть на картинку для збільшення розміру зображення.